Inversión bruta fija privada, producto bruto interno y la tasa de referencia de política monetaria en el Perú: evidencia empírica mediante un modelo VAR (2004-2023)
Private Gross Fixed Investment, Gross Domestic Product and the monetary policy reference rate in Peru: empirical evidence through a VAR model (2004-2023)
Las relaciones entre variables del sector real y monetario son imprescindibles para el diseño y programación de la política económica donde las variables converjan a un comportamiento lineal, homogéneo y parsimonioso. El objetivo es estudiar las relaciones entre la tasa de referencia de la política monetaria, el producto bruto interno (PBI) y la inversión bruta fija privada en el periodo 2004-2023 obtenidos del Banco Central de Reserva del Perú; para ello se estima un modelo de vectores autorregresivos. Se obtuvieron como resultados que el coeficiente de la inversión privada con el PBI del periodo anterior es -0.006, con la inversión privada del periodo anterior es 0.92, con la tasa de referencia del periodo anterior fue -342.9, y con la constante fue de 3610.5. Es importante mencionar que el R² fue de 0.8517. Poner en práctica el segundo objetivo de la modelación VAR, que es la descomposición de la varianza, permitió descomponer la varianza de las variables endógenas en componentes que aislaran el porcentaje de variabilidad de una variable endógena explicada por una de las "innovaciones" para distintos horizontes predictivos. Finalmente, se pudo observar que las variables que participaron en la regresión tuvieron los signos esperados y una adecuada significancia estadística.
The relationships between variables in the real and monetary sectors are essential for the design and planning of economic policy where variables converge to linear, homogeneous, and parsimonious behavior. The objective is to study the relationships between the monetary policy reference rate, gross domestic product (GDP), and private gross fixed investment for the quarterly period 2004-2023, obtained from the Central Reserve Bank of Peru; for this purpose, an autoregressive vector model is estimated. The results obtained show that the coefficient of private investment with GDP for the previous period is -0.006, with private investment for the previous period is 0.92, with the reference rate for the previous period was -342.9, and with the constant was 3610.5. It is important to mention that the R² was 0.8517. By implementing the second objective of VAR modeling, variance decomposition, we were able to decompose the variance of endogenous variables into components that isolate the percentage of variability in an endogenous variable explained by one of the "innovations" for different prediction horizons. Finally, it was observed that the variables included in the regression had the expected signs and adequate statistical significance.
Introducción
Se revisaron algunos trabajos de investigación, que se tomaron como referencia para la realización del presente artículo. En la búsqueda de enfoques que nos brindaran una mejor claridad, se encontró un trabajo de la revista Financial Innovation; en esa investigación los autores (Shi et al., 2021) establecen una relación entre variables del sector real con variables del sector monetario, se enfocan —según los últimos datos publicados por el Banco Popular de China—, en los activos totales de las instituciones financieras, que alcanzaron los 318.69 billones de yuanes a fines de 2019, mientras que las instituciones bancarias representaron el 91%.
Esto muestra que la industria bancaria juega un papel importante en la promoción del crecimiento económico y la prosperidad al proporcionar servicios financieros y de crédito a otros sectores económicos. Los bancos comerciales de China requieren un análisis de la eficiencia de los bancos comerciales en un contexto macroeconómico de crecimiento del producto bruto interno (PIB). La investigación sobre este tema podría promover el avance rápido y saludable de los negocios de financiamiento e inversión de los bancos comerciales y ayudarlos a adaptarse mejor al complejo entorno externo, al tiempo que apoyar el desarrollo estable de la economía nacional (Shi et al., 2021, p. 2).
China no fue inmune a la crisis financiera mundial (GFC). Experimentó una severa desaceleración del crecimiento y, como la mayoría de las economías occidentales, no se ha puesto al día con su tasa de crecimiento tendencial anterior. El modelo de los autores Le et al. (2021) sugiere que los principales shocks que afectaron a China en este período de muestra fueron una combinación de shocks de productividad, inversión y exógenos (fiscales y comerciales), pero que los shocks financieros fueron solo un contribuyente modesto.
Durante el período de la crisis financiera mundial, el sistema bancario estatal, junto con el gasto público directo, se utilizó para complementar agresivamente la política monetaria y compensar la posible desaceleración del crecimiento del PIB. El modelo se utiliza para estimar la frecuencia con la que podríamos esperar ver una desaceleración del crecimiento en China y la frecuencia con la que tales desaceleraciones son impulsadas por shocks financieros (Le et al., 2021, p. 3).
Para el caso de Colombia, un país muy cercano al Perú, los efectos macroeconómicos de la política fiscal y de las variables del sector real no han recibido suficiente atención por parte de los analistas. Poco se sabe sobre los efectos sobre el consumo y la inversión privados derivados de las reiteradas reformas tributarias que se vienen implementando desde mediados de los años ochenta del siglo pasado. Para este caso, toman un modelo VAR estructural de cinco variables, que incluye datos trimestrales sobre el PIB real ($y_t$), el gasto público real en bienes y servicios ($g_t$), los ingresos fiscales netos reales ($t_t$), la inflación ($\pi_t$) medido por el índice de precios al consumidor y las tasas de interés nominales a corto plazo ($r_t$).
También se especificaron modelos VAR estructurales de seis variables, agregando, a su vez, el consumo privado real ($C_t$), la inversión privada real ($I_t$) el empleo (horas trabajadas) ($L$), y el salario real ($W_t$) al conjunto de variables (Lozano y Rodríguez, 2009). Recolectando las cinco variables endógenas en el vector kdimensional $Y_t$, la forma reducida del modelo VAR se puede escribir como:
Dados estos antecedentes previos el objetivo de la investigación es verificar que para el caso peruano las variables del sector real con las del sector monetario guardan una retroalimentación recursiva que puede calibrarse mediante la especificación y posterior calibración de un modelo VAR estructural, así como estimar el impacto que tienen las variables del VAR cuantificadas mediante la estimación de la función impulso-respuesta y qué porcentaje de estas se reflejan sobre las trayectorias temporales mediante la estimación de la función de descomposición de la varianza del error de predicción.
La hipótesis que se postula es que tanto la tasa de referencia de la política monetaria como el producto bruto interno actúan como mecanismo de transmisión (entiéndase "impulso fiscal y monetario") sobre la inversión bruta privada, de manera que identificados los coeficientes para cada una de las variables del VAR se puedan utilizar en posteriores simulaciones de políticas públicas y evaluar la pertinencia de su aplicación. Lógicamente, y en virtud de los fundamentos de la teoría macroeconómica, la evidencia empírica revelada tendrá efectos positivos sobre la tasa de empleo, el consumo privado y el crecimiento económico.
La investigación se justifica en el hecho de que, una vez probada la hipótesis, el VAR se pueda implementar para evaluar el impacto de políticas públicas sobre variables tales como inversión bruta fija privada, producto bruto interno y tasa de referencia de la política monetaria. Asimismo, constituirá un punto de partida para investigaciones más profundas sobre el tema.
Metodología y Datos
La investigación está asociada con el trabajo de Christopher Sims (1980), el cual hace menor uso de la teoría económica que los constructores de modelos macroeconómicos y se ha concentrado en investigar la relación entre los fundamentos económicos de las series de tiempo usando modelos autorregresivos y muchas de las técnicas desarrolladas por el trabajo de Box y Jenkins (1960). Por ejemplo, un modelo simple VAR de la relación entre el ingreso ($Y$) y el dinero ($M$) sería el siguiente:
Yt = β11 + β12Mt-1 + β13Yt-1 + μ1t
Mt = β21 + β22Mt-1 + β23Yt-1 + μ2t
La metodología VAR es, en cierta forma, una respuesta a la imposición de restricciones a priori que caracteriza a los modelos econométricos convencionales: en un sistema de ecuaciones simultáneas se requiere imponer restricciones sobre sus parámetros para garantizar la identificación (condición de orden y de rango) y posible estimación de las ecuaciones que lo conforman. Para ello, además, es indispensable diferenciar entre las variables endógenas y las predeterminadas, es decir, aquellas cuyos valores no son determinados por el modelo en el período actual.
Estas últimas pueden ser exógenas o endógenas rezagadas. El VAR presenta, alternativamente, un sistema de ecuaciones simultáneas en el que cada una de las variables son explicadas por sus propios rezagos y los del resto de variables del sistema. Es decir, no se admiten restricciones a priori y todas las variables son consideradas endógenas. La única información a priori que se incluye está referida al número de rezagos de las variables explicativas que se incorporan en cada ecuación.
Es por ello que la metodología empleada para la realización del presente artículo es la del modelo de auto regresión vectorial (Modelo VAR), la cual tiene fundamento teórico en una estructura vectorial que supone una interdependencia entre las variables del modelo y sus rezagos. Para ello es de vital importancia considerar categóricamente la teoría económica para notar la diferenciación entre las variables antes de estimar el presente modelo.
Una de las principales contribuciones de los modelos VAR en el análisis de series de tiempo es que permite analizar el impacto dinámico de una perturbación no anticipada en una de las variables del sistema sobre las demás. Este análisis se realiza por medio de la estimación de funciones de impulso-respuesta y de descomposiciones de varianza (Morán, 2014).
Por otro lado esta modelación trabaja con información estadística de carácter trimestral para las variables que conforman el VAR y siendo el objetivo de la modelación el cómputo de la función impulso-respuesta y de descomposición de la varianza del error de predicción, no se hace necesario la calibración de un vector de corrección de errores (VEC) o el análisis de estacionariedad típico propuesto por Dickey y Füller o, profundizando un poco más (que no es el objetivo de este artículo), la verificación de ciclo y tendencia del tipo Hodrick y Presscot, Cristiano y Fitzgerald o el filtro propuesto por Kalman, así como la aplicación de pruebas del tipo Zivot y Andrews, puesto que el tradicional test de Dickey y Füller esta sesgado hacia la derecha (es decir, al rechazo de la hipótesis nula) al no considerar la condición de "estabilidad" o, mejor dicho, "quiebre estructural" en la trayectoria temporal de la serie de tiempo; o simplemente a fin de evaluar la condición de cointegración, puesto que este tipo de tratamiento econométrico tiene su fundamento cuando el objetivo de la modelación es el análisis del equilibrio de largo plazo de las variables que conforman el VAR (equilibrio del tipo "punto de silla") y/o el análisis del impacto sobre las variables objetivo ante un shock aleatorio (entiéndase "efectos del tipo transitorio o permanentes"); además de esto un requisito indispensable es que la frecuencia de datos a trabajar permita la detección de patrones tales como tendencias, ciclos, estacionalidades y/o irregularidades; patrones que se obtienen cuando la periodicidad de la frecuencia de datos es mensual.
Por lo anteriormente citado, la mejor propuesta metodológica es el modelo VAR estructural. La forma estructural del VAR parte de la siguiente ecuación (la cual tiene como periodo un análisis trimestral desde 2004.Q1-2023.Q1, recopilando información del Banco Central de Reserva del Perú - BCRP):
Iprivadat = β0 + β1*PBIt + β2*Treft + μt
Donde las variables:
- Iprivada: inversión bruta fija privada, la inversión bruta fija del sector privado se obtiene por diferencia entre la inversión bruta fija total de las cuentas nacionales del Instituto Nacional de Estadística e Informática (INEI) y la inversión pública obtenida de las cuentas fiscales (Banco Central de Reserva del Perú [BCRP], 2011).
- PBI: producto bruto interno, valor total de la producción corriente de bienes y servicios finales dentro de un país durante un periodo de tiempo determinado. Incluye por lo tanto la producción generada por los nacionales y los extranjeros residentes en el país (BCRP, 2011).
- Tref: tasa de referencia de la política monetaria, tasa de interés objetivo para las operaciones interbancarias que el Banco Central procura lograr mediante sus instrumentos de política monetaria, esto es, operaciones de mercado abierto, facilidades de crédito y depósito (BCRP, 2011).
Resultados y Discusión
| IPRIVADA | IPUBLICA | PBI | TIAMN | TIPMN | TREF | |
|---|---|---|---|---|---|---|
| IPRIVADA | 1 | 0.719608 | 0.922625 | 0.838677 | 0.411825 | -0.116290 |
| IPUBLICA | 0.719608 | 1 | 0.890329 | -0.55781 | -0.319735 | -0.119234 |
| PBI | 0.922625 | 0.890329 | 1 | -0.91529 | -0.417252 | -0.258110 |
| TIAMN | -0.838677 | 0.557810 | 0.915290 | 1 | 0.629971 | 0.4952420 |
| TIPMN | -0.411825 | 0.319735 | 0.417252 | 0.629971 | 1 | 0.8748290 |
| TREF | -0.116290 | 0.119234 | 0.258110 | 0.495242 | 0.874829 | 1 |
| Fuente: base de datos empleada (BCRP). | ||||||
Análisis: La evidencia empírica demuestra que la IPRIVADA es directamente proporcional con las variables de la IPUBLICA y el PBI. Sin embargo, para las variables de la TREF, TIAMN y TIPMN la proporción es inversa.
| Dependent Variable: IPRIVADA Method: Least Squares Date: 10/03/25 Time: 21:49 Sample: 2004Q1 2021Q2 Included observations: 70 | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| C | -8982.966 | 1645.521 | -5.459040 | 0.0000 |
| PBI | 0.255394 | 0.012309 | 20.74815 | 0.0000 |
| TREF | 587.8365 | 207.5477 | 2.832296 | 0.0061 |
| R-squared | 0.867144 | Mean dependent var | 19730.80 | |
| Adjusted R-squared | 0.863178 | S.D. dependent var | 6362.416 | |
| S.E. of regression | 2353.422 | Akaike info criterion | 18.40704 | |
| Sum squared resid | 3.71E+08 | Schwarz criterion | 18.50340 | |
| Log likelihood | -641.2464 | Hannan-Quinn criter. | 18.44532 | |
| F-statistic | 218.6527 | Durbin-Watson stat | 0.376818 | |
| Prob(F-statistic) | 0.000000 | |||
| Fuente: base de datos empleada (BCRP). | ||||
Análisis: Podemos observar que, en la tabla observada, el valor de las variables resulta altamente significativo para las variables producto bruto Interno (PBI) y tasa de referencia (TREF). Por ende, se puede precisar que dichas variables están bien incluidas en el modelo planteado. Por otro lado, observamos que presente un $R^2$ de 0.86 y un F estadístico de 218.65, lo cual nos indica que las variables exógenas incluidas determinan el 86% de la variación de la variable dependiente.
| Vector Autoregression Estimates Date: 10/06/25 Time: 11:37 Sample: 2004Q2 2021Q2 Included observations: 69 Standard errors in ( ) & t-statistics in [ ] | |||
| IPRIVADA | PBI | TREF | |
|---|---|---|---|
| IPRIVADA(-1) | 0.925829 (-0.12872) [ 7.19277] | 0.311043 (-0.43432) [ 0.71616] | 0.0000457 (-0.000028) [ 1.62652] |
| PBI(-1) | -0.006497 (-0.03517) [-0.1847] | 0.837856 (-0.11868) [ 7.05961] | -0.0000162 (-0.0000077) [-2.10524] |
| TREF(-1) | -342.9641 (-238.235) [-1.43961] | -857.2949 (-803.859) [-1.06647] | 0.909124 (-0.05199) [ 17.4856] |
| C | 3610.53 (-2089.39) [ 1.73551] | 14841.06 (-7019.71) [ 2.1142] | 1.068253 (-0.45403) [ 2.35283] |
| R-squared | 0.851781 | 0.879724 | 0.863182 |
| Adj. R-squared | 0.84494 | 0.874173 | 0.85686 |
| Sum sq. resids | 3.93E+08 | 4.48E+09 | 18.73219 |
| S.E. equation | 2459.797 | 8299.92 | 0.536831 |
| F-statistic | 124.5137 | 158.4745 | 136.6944 |
| Log likelihood | -634.587 | -718.5025 | -52.92348 |
| Akaike AIC | 18.50977 | 20.9421 | 1.649956 |
| Schwarz SC | 18.63928 | 21.07162 | 1.779469 |
| Mean dependent | 19900.88 | 105211.9 | 3.423913 |
| S.D. dependent | 6246.69 | 23398.42 | 1.418653 |
| Determinant resid covariance (dof adj.) | 3.72E+13 | ||
| Determinant resid covariance | 3.11E+13 | ||
| Log likelihood | -1365.54 | ||
| Akaike information criterion | 39.92868 | ||
| Schwarz criterion | 40.31722 | ||
| Number of coefficients | 12 | ||
| Fuente: base de datos empleada (BCRP). | |||
Análisis: Observamos que el coeficiente del PBI con el PBI del periodo anterior es 0.83 y es altamente significativo. El coeficiente del PBI con la inversión bruta fija privada del periodo anterior es de 0.31. El coeficiente del PBI con la tasa de referencia del periodo anterior fue -875 y tampoco fue significativo. El coeficiente del PBI con la constante fue de 14841.06 y sí fue altamente significativo. Es importante mencionar que el $R^2$ tuvo un valor del 0.8797 y un $R^2$ ajustado de 0.8741. Por otro lado, el coeficiente de la inversión privada con el PBI del periodo anterior es -0.006 y no fue altamente significativo. El coeficiente la inversión privada con la inversión privada del periodo anterior es 0.92, y sí fue altamente significativo. El coeficiente de la inversión privada con la tasa de referencia del periodo anterior fue -342.9 y tampoco fue significativo. El coeficiente de la inversión privada con la constante fue de 3610.5 y no fue altamente significativo. Es importante mencionar que el $R^2$ tuvo un valor del 0.8517 y un $R^2$ ajustado de 0.8449. Finalmente, se puede indicar que el coeficiente de la tasa de referencia con el PBI del periodo anterior es de -0.0000162 y es altamente significativo. El coeficiente de la tasa de referencia con la inversión privada del periodo anterior es 0.0000457, no significativo. El coeficiente de la tasa de referencia con la tasa de referencia del periodo anterior fue 0.90 y altamente significativo. Es importante mencionar que el $R^2$ tuvo un valor de 0.8631 y un $R^2$ ajustado de 0.8568.
| DET_A | 0.000314 | ||
| Fuente: base de datos empleada (BCRP). | |||
Análisis: Según lo observado, se puede mencionar que el valor del determinante es 0.000314, el cual es muy pequeño; es decir, el determinante de la matriz de correlación es bastante cercano a cero. Por ende, se podría decir con certeza que existe presencia de multicolinealidad significativa en la matriz de información de las variables, que afecta su significancia estadística.
Función Impulso-Respuesta
Análisis del impulso-respuesta
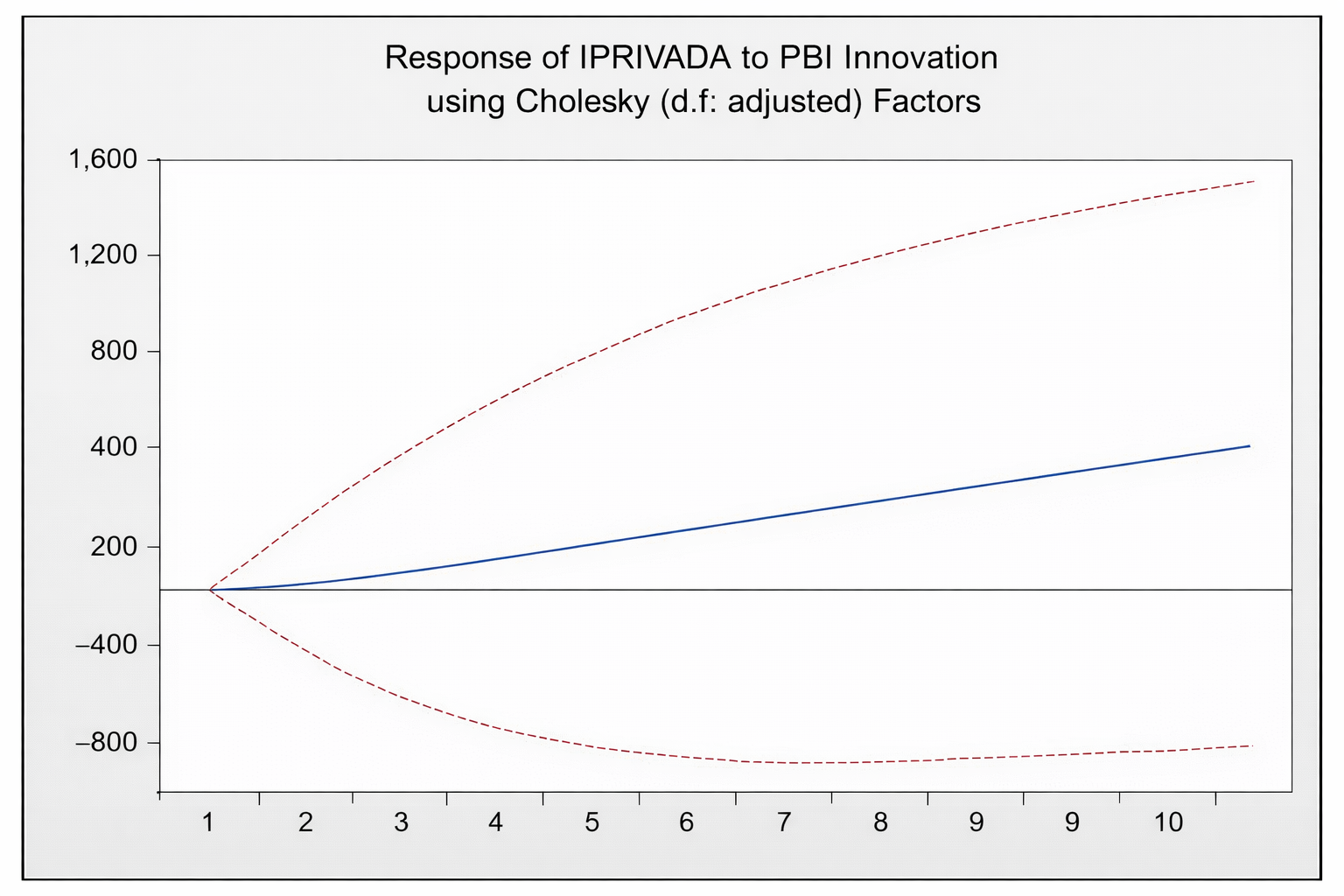
Fuente: BCRP.
Análisis Gráfico 1: Se observa un impacto positivo de la IPRIVADA para los diez periodos de pronóstico. Es decir, existe un shock en el PBI que genera un aumento de la IPRIVADA.
Inversión privada y TREF
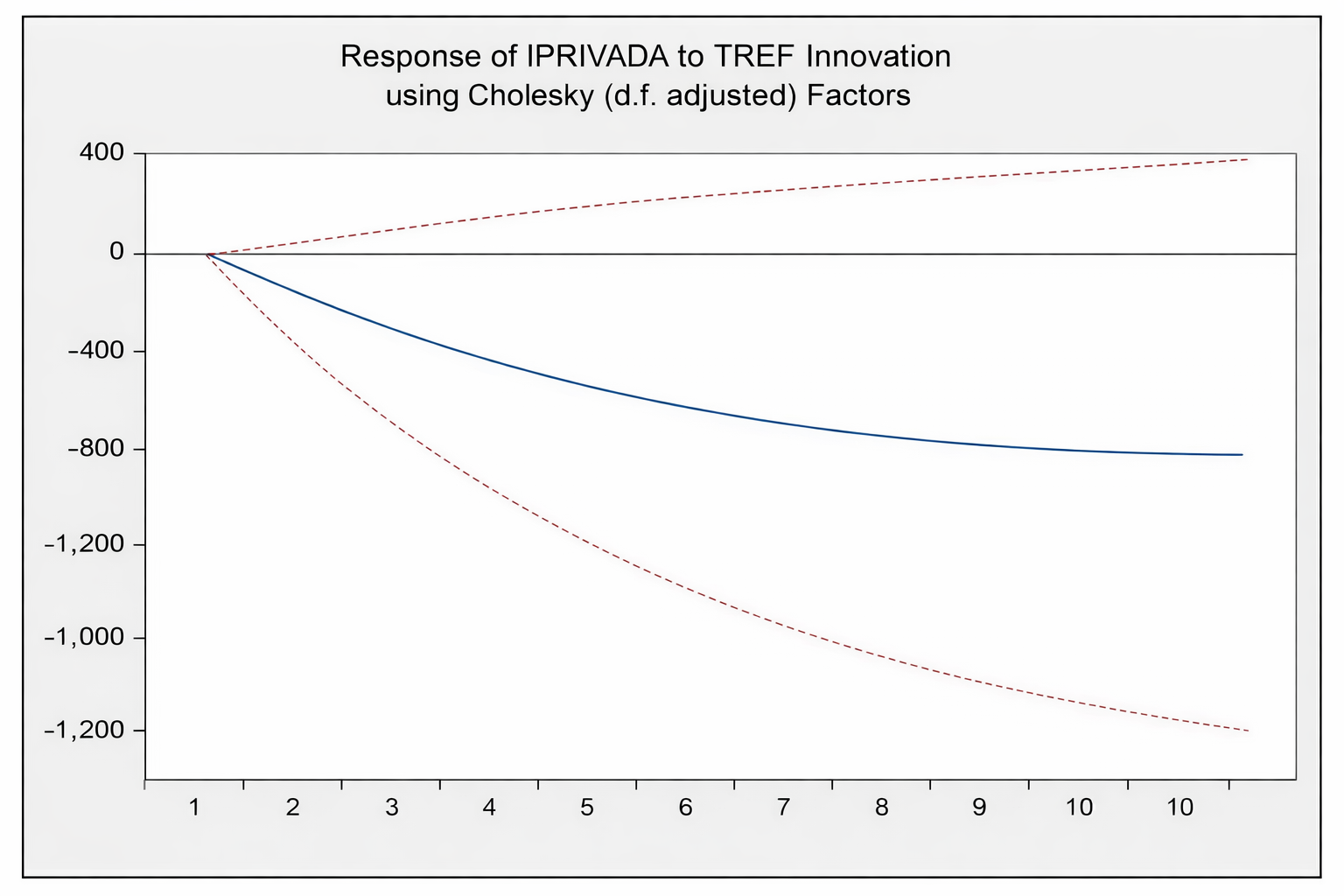
Fuente: BCRP.
Análisis Gráfico 2: En el segundo gráfico, se observa un impacto negativo de la IPRIVADA para los diez periodos de pronóstico. Es decir, existe un shock en la TREF que genera una disminución de la IPRIVADA.
Matriz de respuestas
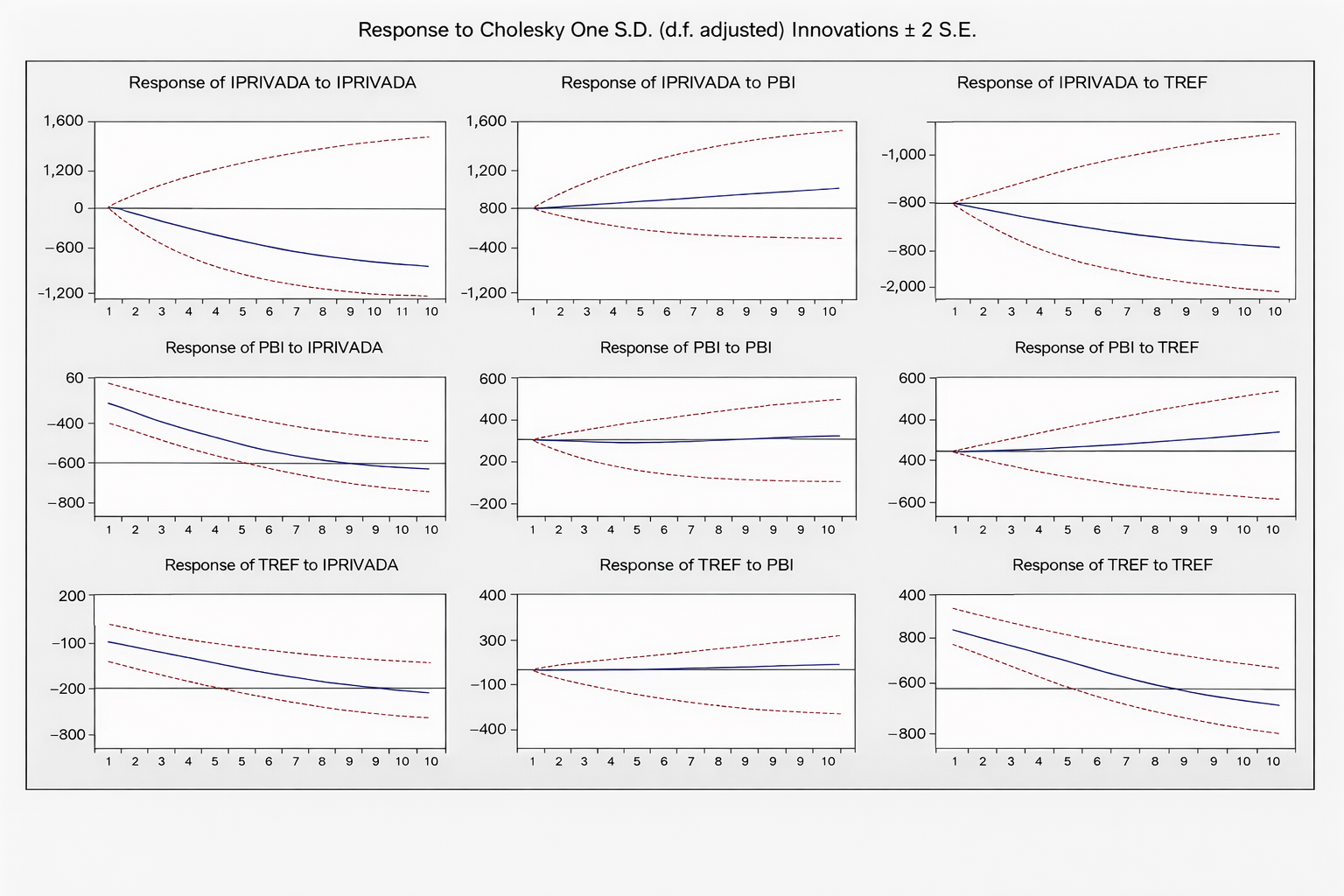
Fuente: BCRP.
Análisis Impulso-Respuesta Tabla VAR
| Response of IPRIVADA: | |||
|---|---|---|---|
| Period | IPRIVADA | PBI | TREF |
| 1 | 2459.797 | 0.000000 | 0.000000 |
| 2 | 2195.707 | -2.307974 | -177.9405 |
| 3 | 1956.479 | 23.98554 | -323.6227 |
| 4 | 1741.844 | 69.60857 | -440.9571 |
| 5 | 1550.906 | 127.2568 | -533.6350 |
| 6 | 1382.338 | 191.2726 | -605.0800 |
| 7 | 1234.537 | 257.3637 | -658.4211 |
| 8 | 1105.744 | 322.3575 | -696.4811 |
| 9 | 994.1371 | 383.9901 | -721.7771 |
| 10 | 897.8999 | 440.7256 | -736.5301 |
| Fuente: base de datos empleada (BCRP). | |||
Para la Tabla 5 el impacto del PBI sobre la variable IPRIVADA en los diez periodos de pronóstico que se ha escogido como marco temporal, se puede apreciar que dicho impacto es positivo y presenta valores fuertes que se van incrementado a medida que van avanzando los periodos. Respecto del impacto de la variable TREF sobre la variable IPRIVADA en los diez periodos de pronóstico, se aprecia que dicho impacto es negativo y presenta valores que se van incrementado negativamente a medida que van avanzando los periodos.
|
TABLA N°6 ANÁLISIS DE LA TABLA DE IMPULSO DE LA VARIABLE PBI |
|||
|---|---|---|---|
| Response of PBI: | |||
| Period | IPRIVADA | PBI | TREF |
| 1 | 6787.525 | 4776.837 | 0.000000 |
| 2 | 6358.214 | 4074.106 | -444.7914 |
| 3 | 5922.583 | 3544.256 | -832.3887 |
| 4 | 5493.222 | 3153.083 | -1164.897 |
| 5 | 5079.167 | 2671.093 | -1445.509 |
| 6 | 4686.689 | 2675.895 | -1678.112 |
| 7 | 4319.685 | 2545.632 | -1866.992 |
| 8 | 3980.366 | 2464.443 | -2016.597 |
| 9 | 3669.574 | 2418.964 | -2131.364 |
| 10 | 3387.142 | 2398.476 | -2215.589 |
| Fuente: base de datos empleada (BCRP). | |||
En la Tabla 6, respecto del impacto de la variable IPRIVADA sobre el PBI en los diez periodos de pronóstico puede apreciarse que dicho impacto es positivo y presenta valores fuertes que van disminuyendo a media que van avanzando los periodos de pronóstico. Se pueden observar los impactos de las variables TREF sobre la variable PBI: el impacto de TREF sobre el PBI en los diez periodos de pronóstico que se ha escogido como marco temporal; se puede apreciar que dicho impacto es negativo y presenta valores que se van incrementando negativamente a medida que van avanzando los periodos de pronóstico.
|
TABLA N°7 ANÁLISIS DE LA TABLA DE IMPULSO DE LA VARIABLE IPRIVADA |
|||
|---|---|---|---|
| Response of TREF: | |||
| Period | IPRIVADA | PBI | TREF |
| 1 | 0.109483 | -0.083757 | 0.518831 |
| 2 | 0.102235 | -0.153341 | 0.471682 |
| 3 | 0.090517 | -0.205351 | 0.427875 |
| 4 | 0.075973 | -0.242870 | 0.387656 |
| 5 | 0.059883 | -0.268573 | 0.351105 |
| 6 | 0.043222 | -0.284760 | 0.318175 |
| 7 | 0.026716 | -0.293386 | 0.288733 |
| 8 | 0.010887 | -0.296103 | 0.262581 |
| 9 | -0.003904 | -0.294292 | 0.239485 |
| 10 | -0.017428 | -0.289094 | 0.219186 |
| Cholesky Ordering: IPRIVADA PBI TREF | |||
| Fuente: base de datos empleada (BCRP). | |||
En la Tabla 7, respecto del impacto del PBI sobre la variable TREF en los diez periodos de pronóstico, se puede apreciar que dicho impacto es negativo, que siguen esa misma tendencia negativa a medida que van avanzando los periodos. Respecto del impacto de la variable IPRIVADA sobre la variable TREF en los diez periodos de pronóstico, se puede apreciar que dicho impacto es positivo, pero presenta valores que van disminuyendo a medida que van avanzando los periodos.
|
TABLA N°8 ANÁLISIS DE LA DESCOMPOSICION DE LA VARIANZA PARA LA VARIABLE IPRIVADA |
||||
|---|---|---|---|---|
| Variance Decomposition of IPRIVADA: | ||||
| Period | S.E. | IPRIVADA | PBI | TREF |
| 1 | 2459.797 | 100.0000 | 0.000000 | 0.000000 |
| 2 | 3302.029 | 99.70956 | 4.89E-05 | 0.290394 |
| 3 | 3851.820 | 99.07677 | 0.003914 | 0.919316 |
| 4 | 4250.861 | 98.13909 | 0.030028 | 1.830885 |
| 5 | 4558.080 | 96.93290 | 0.104063 | 2.963040 |
| 6 | 4805.170 | 95.49612 | 0.252085 | 4.251799 |
| 7 | 5011.336 | 93.86909 | 0.495517 | 5.635394 |
| 8 | 5188.946 | 92.09406 | 0.848113 | 7.057822 |
| 9 | 5346.203 | 90.21374 | 1.314834 | 8.471424 |
| 10 | 5488.608 | 88.26943 | 1.892271 | 9.838295 |
| Fuente: base de datos empleada (BCRP). | ||||
En la Tabla 8 puede observarse que en el primer periodo de pronóstico, para la descomposición de términos de intercambio, el PBI determina un 0%, la TREF un 0% y la misma variable participa con un 100% (es decir, se explica por sí misma). Sin embargo, es importante mencionar que a medida que avanzan los periodos, dicha variable (IPRIVADA) pierde fuerza y se rige de las otras variables. Por ejemplo, en el último periodo la que determina es el TREF, aunque todavía no superaría el valor alcanzado por IPRIVADA.
|
TABLA N°9 ANÁLISIS DE LA DESCOMPOSICION DE LA VARIANZA PARA LA VARIABLE PBI |
||||
|---|---|---|---|---|
| Variance Decomposition of PBI: | ||||
| Period | S.E. | IPRIVADA | PBI | TREF |
| 1 | 8299.920 | 66.87675 | 33.12325 | 0.000000 |
| 2 | 11229.95 | 68.58790 | 31.25523 | 0.156876 |
| 3 | 13207.70 | 69.69276 | 29.79664 | 0.510601 |
| 4 | 14694.14 | 70.28133 | 28.67768 | 1.040996 |
| 5 | 15876.15 | 70.44102 | 27.83823 | 1.720752 |
| 6 | 16852.11 | 70.25268 | 27.22852 | 2.518808 |
| 7 | 17681.04 | 69.78867 | 26.80817 | 3.403154 |
| 8 | 18401.16 | 69.11231 | 26.54467 | 4.343020 |
| 9 | 19038.45 | 68.27792 | 26.41166 | 5.310422 |
| 10 | 19611.14 | 67.33145 | 26.38739 | 6.281157 |
| Fuente: base de datos empleada (BCRP). | ||||
En la Tabla 9 puede observarse que en el primer periodo de pronóstico, para la descomposición de términos de intercambio, la IPRIVADA determina un 66.87%, la TREF un 0% y la misma variable participa el 33.12%. Sin embargo, es importante mencionar que a medida que avanzan los periodos, dicha variable (PBI), pierde potencia y se ve influenciada por las otras variables. Por ejemplo, en el último periodo la que determina es la IPRIVADA, la que ejerce más presión sobre el pronóstico.
|
TABLA N°10 ANÁLISIS DE LA DESCOMPOSICION DE LA VARIANZA PARA LA VARIABLE TREF |
||||
|---|---|---|---|---|
| Variance Decomposition of TREF: | ||||
| Period | S.E. | IPRIVADA | PBI | TREF |
| 1 | 0.536831 | 4.159254 | 2.434236 | 93.40651 |
| 2 | 0.737995 | 4.119886 | 5.605313 | 90.27480 |
| 3 | 0.882086 | 3.936856 | 9.343239 | 86.71990 |
| 4 | 0.996549 | 3.665620 | 13.25968 | 83.07470 |
| 5 | 1.091834 | 3.354546 | 17.09710 | 79.54836 |
| 6 | 1.173156 | 3.041337 | 20.70074 | 76.25793 |
| 7 | 1.243563 | 2.752852 | 23.98903 | 73.25811 |
| 8 | 1.305065 | 2.506467 | 26.92914 | 70.56439 |
| 9 | 1.359106 | 2.311928 | 29.51885 | 68.16922 |
| 10 | 1.406802 | 2.173167 | 31.77411 | 66.05272 |
| Cholesky Ordering: IPRIVADA PBI TREF | ||||
| Fuente: base de datos empleada (BCRP). | ||||
En la Tabla 10 puede observarse que en el primer periodo de pronóstico, para la descomposición de términos de intercambio, el PBI determina un 2.43 %, la IPRIVADA un 4.15% y la misma variable determina el 93.40%. Sin embargo, es importante mencionar que a medida que avanzan los periodos, dicha variable (TREF) pierde relevancia y es determinada por el movimiento de las otras variables. Por ejemplo, en el último periodo la que determina es el PBI, aunque todavía no superaría el valor alcanzado por la TREF.
Conclusiones
Según el análisis realizado, se puede observar que las variables que participaron en la regresión tuvieron los signos esperados. Además, ello mediante se aprecia que las variables PBI, TREF e IPRIVADA presentaron una buena relación durante la corrida del modelo VAR, lo cual se puede corroborar con la significancia estadística.
Los resultados de las predicciones en la prueba impulso-respuesta muestran que el impacto del PBI sobre la IPRIVADA se vuelve más significativo a medida que pasan los trimestres. La determinante es muy cercana a cero, esto conlleva mencionar que de la inversa de la matriz de coeficientes se han obtenido los resultados econométricos; sin embargo, los escalares asociados a las pendientes de la tasa de referencia no cumplen con la condición de insesgamiento.
El uso de la metodología VAR proporciona una estrategia de modelización que permite al investigador plantear un conjunto de ecuaciones a partir de la especificación de un modelo econométrico, el hecho de escoger el orden de rezago ideal recae directamente en el determinante de la matriz, pues al incluir demasiados rezagos se podría llevar al determinante vectorial de la matriz a su "singularidad", lo que imposibilitaría el cómputo de los estimadores MCO.
Tradicionalmente se incluye un test "t-Student por bloques" para evaluar el orden de rezago optimo; sin embargo, la evidencia empírica sugiere que el orden de rezago a incluir no debe exceder de dos. Finalmente, la propuesta ensayada en esta investigación puede constituirse como punto de partida para futuras investigaciones más extensas sobre el tema, incluyendo la evaluación de objetivos de mediano-largo plazo que permitan la inclusión de estrategias econométricas tales como pruebas de estacionariedad con quiebre estructural, típicamente ensayadas en escenarios donde la trayectoria de las variables macroeconómicas han presentado saltos bruscos en su horizonte temporal, muchas veces debido al ensayo de políticas económicas heterodoxas que han causado una volatilidad significativa en variables del sector monetario, tales como la inflación, la tasa de interés y el tipo de cambio.
Notas
- Universidad de San Martín de Porres (Perú).↩
Referencias Bibliográficas
- Banco Central de Reserva del Perú (BCRP). (2011). Banco Central de Reserva del Perú. [Obtenido de Glosario BCRP] https://www.bcrp.gob.pe/publicaciones/glosario.html
- Banco Central de Reserva del Perú (BCRP). (2021). [Obtenido de Estadísticas] https://estadisticas.bcrp.gob.pe/estadisticas/series/
- Le, V. P. M., Matthews, K., Meenagh, D., Minford, P., y Xiao, Z. (2021). China's market economy, shadow banking and the frequency of growth slowdown. Manchester School, 89(5), 420-444. https://doi.org/10.1111/manc.12318
- Lozano, I., y Rodríguez, K. (2009). Assessing the Macroeconomic Effects of Fiscal Policy in Colombia. Banco de la República de Colombia.
- Morán, D. (2014). Determinantes de la inflación en Ecuador. Economía y Sociedad, 1(31), 53-70.
- Shi, Z., Qin, S., Chiu, Y. ho, Tan, X., y Miao, X. (2021). The impact of gross domestic product on the financing and investment efficiency of China's commercial banks. Financial Innovation, 7(1). https://doi.org/10.1186/s40854-021-00251-3
- Trujillo Calagua, G. (2024). Econometría con Eviews. Fondo editorial de la Universidad de San Martin de Porres.
- Trujillo Calagua, G. (2025). Dinámica macroeconómica. Fondo Editorial de la Universidad Católica de Salta.